Electrician
مهندسی برق-الکترونیک-کنترل-ابزار دقیق-انتقال و توزیع-مکاترونیک-کامپیوتر-مکانیک-ITElectrician
مهندسی برق-الکترونیک-کنترل-ابزار دقیق-انتقال و توزیع-مکاترونیک-کامپیوتر-مکانیک-ITبه هم بستن مقاومت ها
مقدمه
اگر سرهای هر یک دو میله مسی و چوبی را که از نظر هندسی مشابه هستند، به اختلاف پتانسیل یکسانی وصل کنیم، جریانهای حاصل در آنها بسیار متفاوت خواهد بود. مشخصهای از ماده رسانا که در اینجا دخالت دارد مقاومت است. مقاومت میان دو نقطه از یک رسانا را گاهی اوقات مقاوم نیز میگویند و در مدار الکتریکی با نماد --^^^― نمایش میدهند. در کاربردهای عملی در هر مدار چندین مقاومت وجود دارد. این مقاومتها به دو صورت میتوانند به همدیگر متصل شوند: یک حالت اتصال سری یا متوالی است و حالت دوم اتصال موازی میباشد.
قانون اهم
اگر به دو سر یک رسانا اختلاف پتانسیل متغیر V را اعمال کنیم و به ازای هر اختلاف پتانسیل اعمال شده ، جریان گذرنده از مقاومت را اندازه بگیریم و نتیجه این اندازه گیریها را در یک نمودار که محور افقی آن بیانگر اختلاف پتانسیل و محور قائم نشان دهنده جریان است، رسم کنیم، نمودار حاصل خط راستی خواهد بود. این خط راست بیانگر این است که مقاومت این رسانا همواره ثابت است و به ولتاژی که برای اندازه گیری آن اعمال میکنیم، بستگی ندارد. این نتیجه مهم که در مورد رساناهای فلزی صادق است، به قانون اهم معروف است.
قوانین کیرشهف
قوانین کیرشهف که در مورد مدارهای اکتریکی برای تشریح مدار مورد استفاده قرار میگیرند، عبارتند از :
قانون اول
فرض کنید از یک مدار الکتریکی با مقاومت الکتریکی R ، جریان i عبور میکند، هرگاه مقاومت در جهت جریان طی شود، تغییر پتانسیل آن iR- و در جهت مخالف جریان ، تغییر پتانسیل iR- خواهد بود.
قانون دوم
اگر یک منبع نیروی محرکه الکتریکی در جهت نیروی محرکه طی شود، تغییر پتانسیل آن ε+ و در جهت مخالف ، تغییر پتانسیل برابر ε- خواهد بود.
اتصال سری مقاومتها
چند مقاومت موقعی بطور سری به هم بسته شدهاند که مجموع اختلاف پتانسیلهای دو سر هر یک از آنها برابر با اختلاف پتانسیل اعمال شده به دو سر ترکیب باشد. در این حالت مقاومتها پشت سر هم قرارخواهند گرفت. به عنوان مثال ، یک مدار الکتریکی را در نظر بگیرید که شامل منبع نیروی محرکه که الکتریکی ε (باتری) و سه مقاومت به اندازههای R_1 و R_2 و R_3 باشد. همچنین فرض کنید که این مقاومتها بصورت متوالی یا سری در مدار قرار گرفتهاند و ما میخواهیم مقاومت معادل این مدار را پیدا کنیم.
ابتدا یادآوری میکنیم که مقاومت معادل ، مقاومتی است که میتواند جایگزین سه مقاومت شده و نقش آنها را در مدار بازی کند. چون مقاومتها به صورت سری یا متوالی قرارگرفتهاند، لذا مقدار جریانی که از هر یک از مقاومتها عبور میکند، برابر بوده و مجموع اختلاف پتانسیل دو سر هر یک از مقاومتها با اختلاف پتانسیل اعمال شده به دو سر ترکیب آنها برابر خواهد بود. به این ترتیب ، اگر رابطه بین جریان ، اختلاف پتانسیل و مقاومت هر مقاومت را نوشته و رابطه اختلاف پتانسیل کل ترکیب با اختلاف پتانسیل دو سر هر یک از مقاومتها را بنویسیم، به این نتیجه میرسیم که مقاومت معادل برابر با مجموع سه مقاومت خواهد بود. یعنی اگر مقاومت معادل را با R_eq نشان دهیم، در این صورت
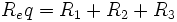
خواهد بود. در حالت کلی ، میتوان گفت که اگر تعداد n مقاومت در یک مدار به صورت سری یا متوالی به همدیگر وصل شده باشند و اندازه مقاومت هر مقاومت با R که اندیس آن مشخص کننده آن است، نشان دهیم، در این صورت مقاومت معادل به صورت زیر در میآید:
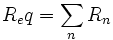
اتصال موازی مقاومتها
اگر چنانچه دو مقاومت به گونهای به یکدیگر وصل شوند که دو سر آنها به هم وصل شود، یعنی اختلاف پتانسیل دو سر آنها با هم برابر باشد، اتصال مقاومتها را اتصال موازی میگویند. برای تشریح این حالت باز یک مثال ساده را در نظر گرفته، سپس نتیجه را در حالت کلی تعمیم میدهیم.
فرض کنید مداری داریم که از یک منبع نیروی محرکه الکتریکی و سه مقاومت به اندازههای R_1 و R_2 و R_3 که به صورت موازی به هم وصل میشوند، تشکیل شده است. هچنین فرض کنید که جریان کل تولید شده توسط منبع i باشد. طبیعی است که در این حالت جریان کل برابر با مجموع جریانهای گذرنده از هر مقاومت خواهد بود. بنابراین اگر جریان گذرنده از مقاومتها را به ترتیب با i_1 و i_2 و i_3 نشان دهیم و اختلاف پتانسیل کل که برابر با اختلاف پتانسیل دو سر هر یک از مقاومتهاست، V باشد، در این صورت چون i= i_1 + i_2 + i_3 است و نیز به دلیل اینکه رابطه جریان و اختلاف پتانسیل هر مقاومت را میتوان به صورت
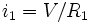 و
و 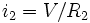 و
و 
نوشت، لذا مقاومت معادل به صورت

خواهد بود. بدیهی است که در حالت کلی ، یعنی ترکیب تعداد n مقاومت (هر مقاومت با اندیس در زیر R مشخص میشود) مقاومت معادل به صورت زیر در میآید:

منبع:http://fizik2.blogveb.com


























