خازن کروی

مقدمه

دو جسم رسانا که بتوانند بارهای مساوی و مختلف العلامه () را در خود ذخیره کنند و اختلاف پتانسیل میان آنها به باردار بودن سایر رساناهای دستگاه بستگی نداشته باشند، تشکیل خازن می‌‌دهند. این بستگی نداشتن به بارها به معنی آن است که یکی از این دو رسانا مانند سپری رسانای دیگر را حفاظت می‌‌کند. به بیان دیگر ، پتانسیلی که بارهای دیگر در هر یک از زوج رساناها ایجاد می‌‌کنند، باید یکسان باشد.

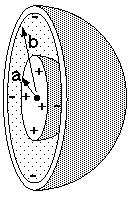
خازن می‌‌تواند با توجه به شکل هندسی رساناهای موجود در آن انواع مختلف داشته باشد. خازن کروی یکی از این نمونه‌ها می‌‌باشد. در خازن کروی همانگونه که از نامش روشن است، رساناها به شکل کره‌های هم مرکز هستند که شعاع یکی از دیگری بزرگتر می‌‌باشد. شکل هندسی خازن فقط منجر به داشتن ظرفیت متفاوت می‌‌گردد، ولی در نوع اتصال خازنها و یا موارد دیگر فرقی ندارد. 

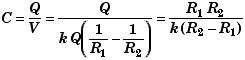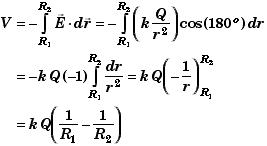ظرفیت خازن کروی

بهترین روش برای تعیین ظرفیت خازن کروی ، با توجه به تقارن موجود در آن استفاده از قانون گاوس است. برای این منظور باید یک سطح فرضی به عنوان سطح گاوسی در نظر بگیریم. به عنوان مثال ، اگر شعاع کره رسانای داخلی r₁ و شعاع رسانای خارجی r₂ باشد، کره فرضی با شعاع r بطوری که r₂ > r > r₁ باشد، در نظر می‌‌گیریم. اگر قانون گاوس را در مورد این کره اعمال کنیم، میدان الکتریکی در فضای میان صفحات از رابطه زیر محاسبه می‌‌شود:

که در آن q مقدار بار ذخیره شده در روی صفحات کروی خازنها است. با در دست داشتن E می‌‌توان اختلاف پتانسیل میان صفحات خازن را تعیین کرد و از آنجا ظرفیت خازن با توجه به رابطه C = qV می‌‌تواند به صورت زیر بیان شود:

کره منزوی

به یک تک رسانای کروی منزوی ، با این فرض که صفحه دیگر کره رسانایی به شعاع بینهایت است، می‌‌توان یک ظرفیت نسبت داد، اما به دلیل اینکه خطوط میدانی که از سطح یک کره رسانای منزوی باردار خارج می‌‌شوند، باید به جایی ختم شوند، می‌‌توان دیواره‌های اتاقی را که رسانا در آن قرار دارد، به عنوان کره مورد نظر با شعاع بینهایت فرض کرد.

برای محاسبه ظرفیت این چنین خازنی ، فقط کافی است که در رابطه ظرفیت خازن کروی شعاع b را به سمت بینهایت میل دهیم. در این صورت ظرفیت کره منزوی به صورت زیر خواهد بود:

وجه مشترک کلیه خازنها

در کلیه خازنها قوانین مربوط به اتصال خازنها به یک صورت است و فقط ظرفیت خازن ، با توجه به تغییر شکل خازن متغیر خواهد بود. همچنین روابط مربوط به محاسبه انرژی خازنها نیز به این صورت خواهد بود. در مورد خازنهای کروی نیز می‌‌توان به جای خلا نوعی ماده دی الکتریک در داخل خازن قرار داد. در این صورت اگر ثابت دی الکتریک ، ماده دی الکتریک مورد نظر را با k نشان دهیم، کافی است که در کلیه روابط بجای ε₀ از کمیت kε₀ استفاده کنیم.

گزارش تخلف
برچسب هاخازن3,

منبع:http://fizik2.blogveb.com